I) Method Development
A) Correlation Corrected Ab Initio Methods
- Development of Sixth Order Perturbation Theory
- Derivation of a Size-Extensive QCI Methods and QCI Methods correct to Sixth Order
- Investigation of the Convergence of the Møller-Plesser (MP) Perturbation Series
- Development of Spin-Projected Coupled Cluster Methods
1. Development of Sixth Order Perturbation Theory
Many-Body Perturbation Theory (MBPT) methods using the Møller-Plesset (MP) perturbation operator has been extensively used in WFT to describe electron correlation effects. Best known are second order MBPT (MBPT2 or MP2), third order MBPT (MBPT3 or MP3), and fourth order MBPT (MBPT4 or MP4). These methods are easy to apply but have the disadvantage that their results oscillate with the order of perturbation theory applied. The really interesting methods are the even-order MBPT methods since they introduce important new correlation effects. The second and fourth order MBPT are available for a long time and are frequently applied. We worked out sixth order MBPT (MBPT6 or MP6: 36 different energy contributions of the type E(ABC) with A,B,C = S, D, T, Q, and P excitations), which turned out to be much more accurate than any lower order MBPT method and which gave for the first time some indication to which limit value MBPT converges at infinite order. We used MP6 to predict full CI energies, to study the convergence behavior of the MP series and to test the accuracy of approximate MP6 methods.
For further reference, see:
- 154Sixth-Order Many-Body Perturbation Theory I. Basic Theory and Derivation of the Energy Formula, Zhi He and D. Cremer, Int. J. Quant. Chem., 59, 15 (1996).
- 155Sixth-Order Many-Body Perturbation Theory II. Implementation and Application, Zhi He and D. Cremer, Int. J. Quant. Chem., 59, 31 (1996).
- 156Sixth-Order Many-Body Perturbation Theory III. Correlation Energies of Size-extensive MP6 Methods, Zhi He and D. Cremer, Int. J. Quant. Chem., 59, 57 (1996).
- 162Sixth Order Møller-Plesset (MP) Perturbation Theory - On the Convergence of the MPn Series, D. Cremer and Zhi He, J. Phys. Chem, 100, 6173 (1996).
- 188Møller-Plesset Perturbation Theory, D. Cremer, Encyclopedia of Computational Chemistry, H.F. Schaefer III, Editor, Wiley, 1998, Vol. 3, p. 1706-1735.
- 210Assessment of Higher Order Correlation Effects with the Help of Møller-Plesset Perturbation Theory up to Sixth Order - Yuan He and D. Cremer, Mol. Phys. 98, 1415-1432 (2000).
- 211Molecular Geometries at Sixth Order Møller-Plesset Perturbation Theory – At What Order Does MP Theory Give Exact Geometries? Yuan He and D. Cremer, J. Phys. Chem. A, 104, 7679-7688 (2000).
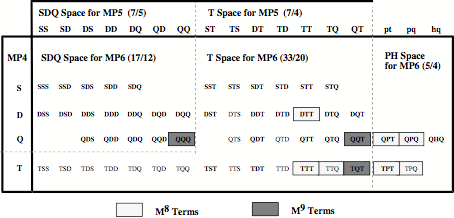
Figure 1. Decomposition of the MP6 energy into different contributions determined by single (S), double (D), triple (T), quaduple (Q), pentuple (P), and hextuple (H) excitations arranged in different spaces: SDQ, T, and PH space. Terms depending on M8 or M9 where M is the number of basis functions are indicated.
2. Derivation of a Size-Extensive QCI Methods and QCI Methods correct to Sixth Order
(Professor Dieter Cremer)
Coupled Cluster (CC) methods have the advantage of covering all correlation effects of a given type up to infinite order and, therefore, they are superior to MBPT methods, however also much more complicated than the latter. CCD, CCSD, and CCSDT exist, where only the first two methods are frequently used whereas the third method has been programmed only by a few groups including us. We have developed as an alternative to CCSDT the quadratic CI method QCISDT, which is cheaper than CCSDT (it converges much faster than CCSDT) but leads to the same accuracy of results as CCSDT. Contrary to previous suggestions of QCISDT, our method is size-extensive. In addition, it is the basis for a hierarchy of size-extensive QCI methods that are computationally attractive.
For further reference, see:
- 136Analysis of Coupled Cluster Methods. IV. Size-extensive Quadratic CI Methods - Quadratic CI with Triple and Quadruple Excitations, D. Cremer and Zhi He, Theoret. Chem. Acta, 88, 47 (1994).
- 139Size-extensive QCISDT - Implementation and Application, D. Cremer and Zhi He, Chem. Phys. Lett., 222, 40 (1994).
- 152Application of Quadratic CI with Singles, Doubles, and Triples (QCISDT): An Attractive Alternative to CCSDT, Zhi He, E. Kraka, and D. Cremer, Int. J. Quant. Chem., 57, 157 (1996).
- 170New Developments in Many Body Perturbation Theory and Coupled Cluster Theory, D. Cremer and Zhi He, in "Conceptual Perspectives in Quantum Chemistry, Volume III", J.-L. Calais and E. Kryachko, Edts, Kluwer Publishing Co, Dordrecht, 1997, p. 239.
- 199Size-extensive Quadratic CI Methods Including Quadruple Excitations: QCISDTQ and QCISDTQ(6) - On the Importance of Four-electron Correlation Effects, Yuan He, Zhi He, and D. Cremer, Chem. Phys. Lett., 317, 535-544 (2000).
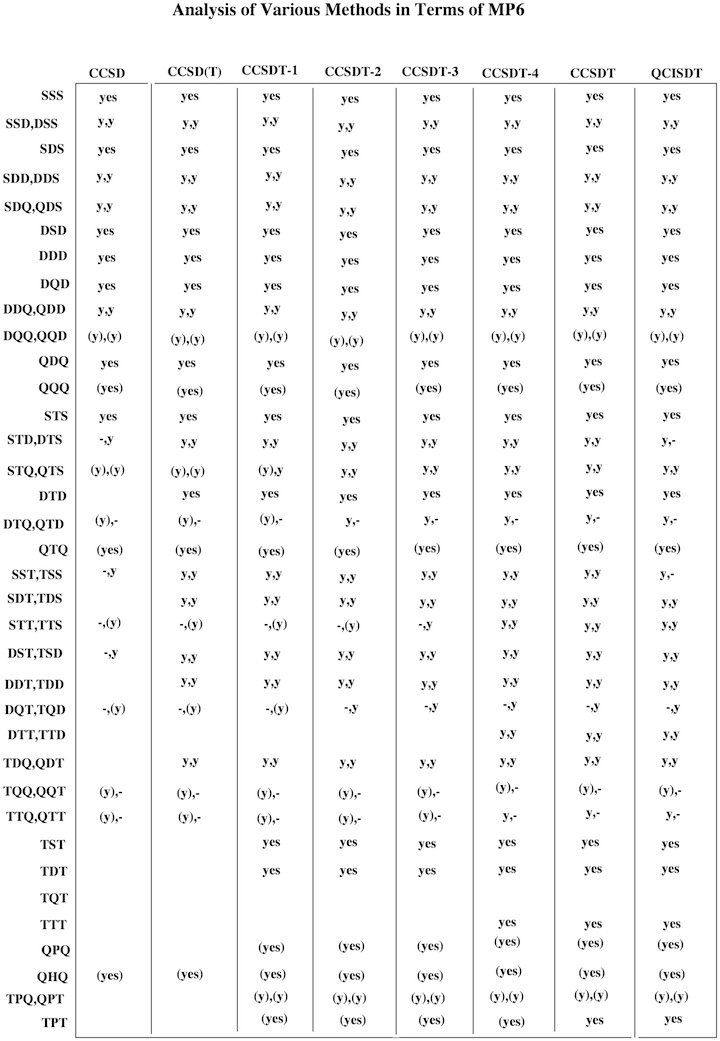
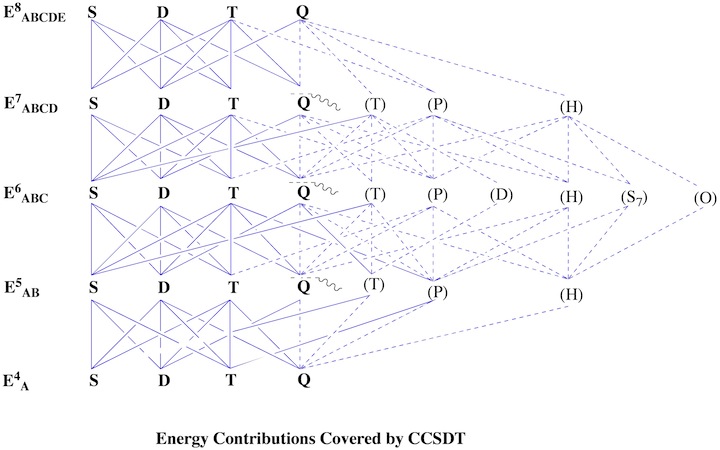
Figure 1. Decomposition of Couple Cluster and Quadratic CI methods in terms of 6th order perturbation theory. The abbreviation y = yes or (y) = (yes) indicate whether the term considered is included fully or just partly. From this information it is possible to predict the reliability and accuracy of a given CC or QCI method.
3. Investigation of the Convergence of the Møller-Plesser (MP) Perturbation Series
(Professor Dieter Cremer)
The most often used correlation corrected ab initio method is Møller-Plesset (MP) perturbation theory. Today it is standard to calculate energy and geometry first at the second order MP (MP2) level of theory before one applies higher levels of MP theory such as MP3, MP4, MP5 or even MP6. While such a procedure was until recently generally accepted to increase the accuracy of calculated energies (MP6 is on the average within 1.7 mhartree of full CI energies in the case of small molecules with one or two heavy atoms), our research revealed that for certain molecules MP energies can oscillate due to an exaggeration of correlation effects at even orders and their underestimation at odd orders, which makes it difficult to assess the accuracy of a MP calculation. Also, it was shown that the MPn series can diverge for seemingly unproblematic single reference molecules. This puts considerable doubt to the physical basis of MP theory and leads to the question whether one should use MP theory for correlation corrected ab initio investigations (see Jeppe Olsen's work).
Due to our work on MP6, we were in the situation to analyze the convergence behavior of the MP series. The work we carried out had three goals: First, we investigated under which circumstances MP energies start to oscillate or even diverge with increasing order. Secondly, we applied various convergence acceleration methods and tested whether one can enforce convergence of the MPn series despite of oscillatory or divergence behavior. Finally, we investigated how from known MP energies independent of the convergence behavior of the MP series reliable predictions of FCI energies can be made that help to obtain chemically relevant energy differences.
For further reference, see:
- 157Improvement of the Møller-Plesset Correlation Energy Series by Using Pade, Feenberg, and other Approximations up to Sixth Order, Zhi He and D. Cremer, Int. J. Quant. Chem., 59, 71 (1996).
- 174Prediction of Full CI Energies with the help of Sixth-Order Møller-Plesst (MP6) Perturbation Theory, D. Cremer and Zhi He, Special Issue for the WATOC Symposium in Jerusalem 1996: J. Mol. Struct. (Theochem) 398-399, 7 (1997).
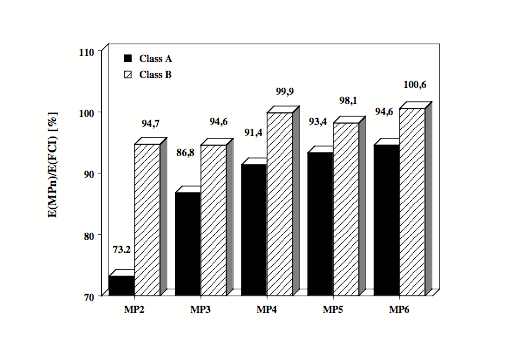
Figure 1. Electronic systems with well-separated electron pairs (class A systems: alkanes, Li, Be, B compounds, etc.) are reasonably described by MP2 and MP4 since electron correlation is dominated in these systems by pair correlation effects. The MP energies of class A systems converge slowly but steadily to the full CI value. - Electronic systems with a clustering of electrons in certain regions of space (class B systems: molecules with electronegative atoms, hypervalent molecules, transition metal complexes, etc.) show complicated electron correlation effects that can only be described by including three-electron and four-electron correlation effects. The MPn energies oscillate for class B systems since at even orders the correlation effects are overestimated and at odd orders they are underestimated. This is shown in the Figure where average dynamic correlation energies calculated for about 30 electronic systems are given from MP2 to MP6 as a fraction of the exact correlation energy.

Figure 2.Considering the different convergence behavior of the MPn series for molecules of classes A and B, it pays out to determine first whether a given molecule belongs either to class A or class B and then to constrain calculations only to those methods, which lead to a substantial improvement of the correlation effects.
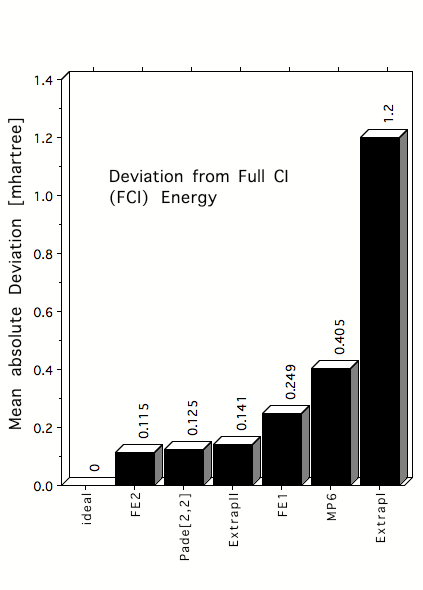
Figure 3. Mean absolute deviations (in mhartree) of estimated FCI correlation energies from exact FCI energies for 22 atoms and molecules in their equilibrium geometry. FCI energies are estimated by first order Feenberg scaling (FE1), second order Feenberg scaling (FE2), [2,2] Pade approximants, MP6 correlation energies or MP6 based extrapolation formulas such as ExtrapII.
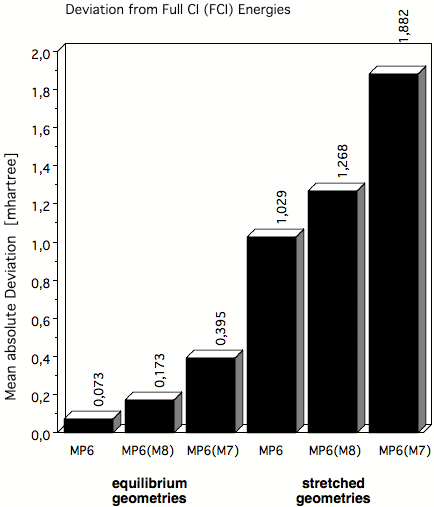
Figure 4. Mean absolute deviations (in mhartree) of MP6 correlation energies from exact FCI energies in the case of molecules at their equilibrium geometry and at stretched geometries where in the latter case multireference effects play an increased role. MP6(M8) and MP6(M7) are apprimations to true MP6 obtained by including only terms up to M8 or M7 where M is the number of basis functions used in the basis set.
4. Development of Spin-Projected Coupled Cluster Methods
Unrestricted Hartree-Fock (UHF) theory has the advantage of describing homolytic dissociation qualitatively correct. If it is used as a starting point for Coupled Cluster (CC) methods, there will be the chance of getting a quantitatively correct description of dissociation reactions with a single determinant description. However, one of the major shortcomings of the UHF method is that the wave function is not an eigenfunction of the spin operator S2. Contaminations from higher spin states with S+1, S+2, etc. (S: total spin of molecule) are mixed into the wave function and lead to erroneous energies that effect the shape of a potential energy surface determined at the UHF level.
We showed that UHF-CCSD and UHF-CCSD(T) benefit from a complete suppression of the S+1 contaminant, which is reflected by the <S2> value in UHF-CC theory provided this is partitioned in an energy and a wave function related part. The S+2 contaminant (e.g., for a singlet biradical the pentuplet state) can be projected out with some extra work thus yielding rather accurate values in situations where other UHF based methods fail.
Approximate spin-projection methods (APCC theory) for UHF-CCSD and UHF-CCSD(T) to project out S+2 and S+3 contaminants (higher contaminants are normally not important) were developed. Such methods have two major advantages: a) The cost for spin projection is just a fraction of the actual UHF-CC calculation. b) UHF-CC theory can be applied in those cases in which otherwise only expensive MR-CC methods are reliable. Accordingly, one can apply APCC methods to study bond dissociation and organic biradicals.
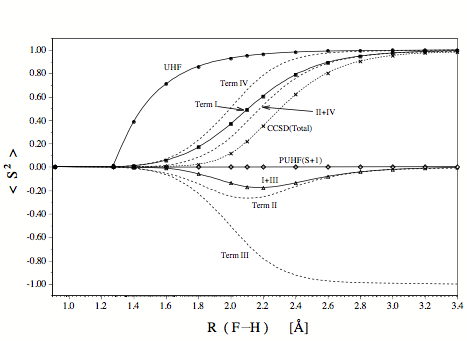
Figure 1. Changes in <S2> calculated at different levels of theory for the stretching of the F-H bond. The expectation value of <S2> is decomposed for CCSD into four terms, two of which result from the form of the energy operator (CCSD energy related terms I and III) and two of which are related to the CCSD wave function (terms II and IV) since they reflect the response of the wave function on the perturbation caused by spin contamination. One could also speak of Hellmann-Feynman terms I and III as well as response terms II and IV.
Some interesting conclusions result from the investigation of terms I, II, III, and IV.
- UHF-CCSD is well-suited to correctly describe single bond breaking because it is free of the S+1 contaminant typical of and problematic for UHF, UMPn, and all UHF-based correlation corrected ab initio methods without infinite order effects.
- The quality of the UHF-CCSD energy is correctly reflected by the energy related term <S2>CCSDI+III, which indicates that region of bond breaking, which suffers most (recoupling region) and least (small R and large R) from spin contamination. Hence, <S2>CCSDI+III rather than <S2>CCSDTotal should be used as a diagnostic for the accuracy of the UHF-CCSD energy.
- The response of the UHF-CCSD wave function will be large if the UHF wave function has a large spin contamination. This is reflected by the wave function related term <S2>CCSDII+IV, which dominates the value of <S2>CCSDTotal. Hence, a large value <S2>CCSDTotal as for example for large distances R in the case of the homolytic dissociation of a single bond is simply the reflection of the fact that the UHF-CCSD wave function does not fulfill the Hellmann-Feynman theorem.
- The energy related term <S2>CCSDI+III reveals that the UHF-CCSD energy will be of less accuracy if two or more bonds are are broken and S+2, S+3, etc. contaminants are included into the wave function. The latter can be projected out by the approximate projection operator A(m) , which helps to identify the most serious spin contaminations.
Since UHF-CCSD theory, contrary to UHF theory, does not suffer from the S+1 contaminant, this level of theory should be appropriate for describing singlet biradicals such as p-benzyne. However, if spin contaminants S+2, S+3, become important at the UHF-CCSD level of theory, then the use of spin projection methods will be advisable. Alternatively, CCSDT or BCCD can be employed since these methods will also reduce the S+2 contaminant.
