I) Method Development
D) Calculation of Magnetic Properties
- Calculation of NMR Chemical Shifts with DFT
- Development of methods for calculating SSCC
- Analysis methods for NMR Spin-Spin Coupling Constants
1. Calculation of NMR Chemical Shifts with DFT
(Professor Dieter Cremer, Professor Elfi Kraka)
If a chemist synthesizes a new compound, one of the first investigations to be carried out will be the measurement of the NMR spectrum. NMR spectral data provide useful information on the identity and the structure of new compounds. In most cases, there exist sufficient reference data that make a qualitative structure determination or verification possible. Only after these first NMR investigations have been done, it is normally decided whether a direct structure determination with other methods is performed. However, these additional investigations require normally much more time and efforts than the NMR measurements and, therefore, they are only done for interesting compounds. This is the reason why for many compounds, there is just a NMR spectrum available that does not provide all the information and insights an experimentalist wants to have on a new compound.
Experimentalists expect additional information from quantum chemical calculations. This is obtained by calculating NMR chemical shifts for some appropriate trial structure and comparing them with existing NMR data. If the two sets of NMR data agree, the compound in question must possess the molecular structure used in the calculation and, therefore, it is positively identified. All the molecular properties that are obtained by the calculation can be assigned to the new compound and, accordingly, the experimentalist gets a detailed description. In this way, the calculation of NMR chemical shifts provides an ideal basis for the collaboration between experimentalists and quantum chemists.
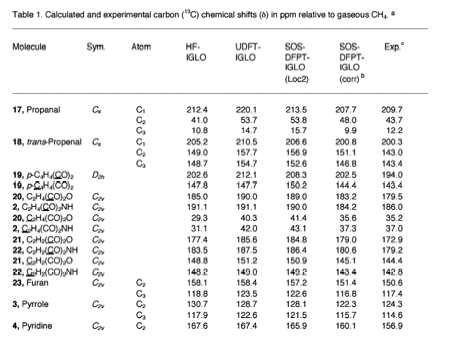
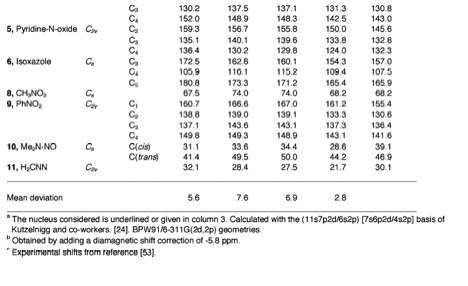
We have successfully used the ab initio/NMR technique for identifying new compounds in several cases, but we were limited by the accuracy of the methods applied. We considered Malkin's idea of a DFT-based method for improving of calculated NMR chemical shifts. Our method starts from an accurately calculated HF exchange part and a numerically determined correlation part in connection with the IGLO formalism. Results are reliable provided Malkin's level shift operators are used in a significantly improved form. We get excellent results for δ13C, δ15N, δ19F, and δ29Si.
For further reference, see:
- 129Calculation of NMR Chemical Shifts - The Third Dimension of Quantum Chemistry, D. Cremer, L. Olsson, F. Reichel, and E. Kraka, Israel J. Chem., 33, 369 (1993).
- 167Sum-over-states Density Functional Perturbation Theory: Prediction of Reliable 13C, 15N, and 17O Nuclear Magnetic Resonance Chemical Shifts, L. Olsson and D. Cremer, J. Chem. Phys. 105, 8995 (1996).
- 168Dimesitylketone O-Oxide: Verification of an Unusually Stable Carbonyl Oxide by NMR Chemical Shift Calculations, E. Kraka, C. P. Sosa, and D. Cremer, Chem. Phys. Lett. 260, 43 (1996).
- 169Prediction of Nitrogen and Oxygen NMR Chemical Shifts in Organic Compounds by Density Functional Theory, L. Olsson and D. Cremer, J. Phys. Chem. 100, 16881 (1996).
2. Development of methods for calculating SSCC
In 2000, we developed the first DFT program that fully calculates NMR spin,spin coupling constants (SSCCs) within the Coupled Perturbed DFT (CPDFT) approach. Similar developments dating to years before 2000 can be found in the literature, however they were based on the programming of just one or three of the four Ramsey terms that determine the value of the SSCC, namely the Fermi contact (FC), the spin-dipole (SD), the paramagnetic spin-orbit (PSO), and the diamagnetic spin-orbit (DSO) term. None of the previous developments succeeded in setting up the SD term and the argument used in this connection was that this term is rather small. This however is only true for hydrocarbons, but as soon as hetero atoms with electron lone pairs are involved, this argument does no longer hold as we could demonstrate for NX, OX, FX coupling constants (X = H, C, N, O, F).
We tested local, nonlocal (GGA), and hybrid functionals, where the latter were optimized for the particular purpose of calculating SSCCs. It turned out that a GGA functional is absolutely necessary to obtain reliable values, however performance can be improved by using a suitable hybrid functional. We designed a hybrid functional that can reproduce experimental SSCC values in a reliable way reaching almost Coupled Cluster accuracy.
In addition to the CPDFT method Sum-over-states density functional perturbation theory (SOS-DFPT) and Coupled perturbed Hartree-Fock (CPHF) programs were set up to have also methods available, which were used in the past to calculate SSCC values.
SSCCs were calculated with CPDFT, EOM-CCSD, CCSD, CPHF, and SOS-DFPT where CCSD was used for accurate descriptions and CPDFT forlarge scale calculations of indirect SSCCs.
For typical hydrocarbons and other typical first row molecules containing hetero atoms such as N, O, F, we investigated the electronic mechanism, which determines the sign and the magnitude of the SSCC. One finds in the literature similar studies, however they normally concentrate just on the FC term, which dominates often but not always the value of the SSCC. We could demonstrate under which conditions SD and PSO term become also important.
3. Development and Application of a New Method for a Systematic Analysis of NMR Coupling Constants: J-OC-PSP
A) How it started?
Although the analysis and the understanding of spin-spin coupling constants J has been continuously improved since the 70ies (in particular in the case of hydrocarbons), it is still a difficult task to analyze J constants, in particular when heteroatoms participate in the coupling mechanism. J values (or better reduced coupling constants K) are sensitive to so many aspects of molecular structure that the details tend to obscure the general nature of the coupling mechanism. Attempts have been made to dissect K into orbital contributions, however these attempts are limited or flawed in one or another way and are mostly focused on the Fermi contact term rather than the total reduced coupling constant K. Goal of the project is to derive/program a better method for dissecting K into orbital contributions that provide a basis for relating K to electronic structure features and analyzing its geometrical dependence.
There have been various attempts to dissect the reduced spin-spin coupling constant K into orbital contributions. We programmed the NBO (natural bond orbital) analysis of J, but were not satisfied by this approach. [1] The NBO approach considers just the Fermi Contact (FC) term of K and disregards spin-dipole, diamagnetic and paramagnetic spin orbit (SD, DSO and PSO) contributions to K. In particular, SD and PSO contributions can add considerably to K and, therefore, have to be analyzed to understand the magnitude of the reduced coupling constant. Therefore, it is planned to develop an analysis method that is based on the complete theory of reduced coupling constants and that gives for each contribution to K a decomposition into one-orbital and two-orbital terms describing repolarization, delocalization, and exchange repulsion interactions triggered by induced local magnetic fields in a molecule. In this way, the influence of spin-polarization and orbital currents can be described. The theory of the new analysis method has been worked out and an appropriate computer program has to be written.
The new method will be applied on a routine basis. Apart from this, several subprojects will focus on the coupling mechanism in selected cases that are not well understood so far.
a) Presently, there is a controversial discussion to which extends through-space interactions can contribute to the magnitude of spin-spin coupling constants. Using the new orbital analysis program, we will investigate J(N,F) coupling constants of organic molecules in which N and F are sterically close to each other although they are separated by a long bond path. In this connection, we will calculate NMR spin-spin coupling constants J(N,F) of fluorinated phenyl oximes. The orbital analysis of calculated K values will provide a basis to distinguish between a through-space and through-bond coupling mechanisms.
b) One-, two-, and three-bond coupling constants J(X,Y) provide the most direct information on molecular structure. However, the relationships between, electronic structure, molecular geometry, and 1,2J coupling constants are less well-understood than those valid for three-bond interactions, in particular if X or Y represent heteroatoms. For combinations of 1H, 13C, 15N, 17O and 31P nuclei, a systematic investigation will be carried out to clarify the dependence of 1J and 2J coupling constants on bonding, electronic structure, and geometry parameters, the nature and orientation of neighboring bonds, the vicinity and orientation of electron lone-pairs, electron-delocalization effects (anomeric, hyperconjugative, p-conjugative), the electric field effect of a neighboring positive/negative charge as well as unspecific and specific solvation.
The goal of this work will be to establish a number of simple relationships between coupling constants and geometrical parameters, which we need for the investigation of biochemical compounds such as nucleotides, DNA, polypeptides, proteins, etc.
B) The present status: What has been accomplished?
When a new chemical compound is synthesized, one of the first investigations to be carried out is the measurement of the Nuclear Magnetic Resonance (NMR) spectrum. Because of the sensitivity of NMR parameters such as NMR chemical shifts or NMR spin-spin coupling constants (SSCC) to structural and conformational features of a molecule, NMR spectral data provides in relatively easy way useful information on the identity and the structure of the new compound. There exists in most cases sufficient reference data that makes a qualitative structure determination or verification possible. This is the reason why for many compounds, there is just an NMR spectrum available that has to provide all the information and insights an experimentalist wants to have on a new compound.
The information content of an NMR spectrum can be extended and completed with the help of quantum chemical calculations of NMR parameters. This is best done when for some appropriate trial structure NMR chemical shifts and SSCCs are calculated and compared with the existing NMR data. If the two sets of NMR data agree, the compound in question will possess the molecular structure used in the calculation and, therefore, is positively identified. All molecular properties determined in the calculation can be assigned to the new compound and, accordingly, the experimentalist gets a detailed description of the compound in question.
We were the first to develop a new, reliable, and very economic quantum chemical method of calculating NMR SSCCs with the help of density functional theory (DFT). In recent time our method has been adopted by numerous other groups and is presently considered to be the standard for quantum chemical calculations of SSCCs. Also, we have demonstrated how the calculation of SSCCs can substantially aid the understanding of the spin-spin coupling mechanism and thereby increase the value of SSCCs as structural and conformational descriptors of molecules. Quantum chemistry can advance the analysis of SSCCs to a point that the information content of SSCCs also with regard to the electronic structure of a molecule becomes accessible. The SSCC between two nuclei depends on the distribution of electrons in a bond or a chain of bonds connecting these nuclei and, therefore, it indirectly describes the bonding situation of the molecule under investigation.
With the routine calculation of fairly accurate SSCCs based on DFT, there is for the first time the possibility of assessing electronic structure features in a systematic way directly from routinely computed SSCCs. For this purpose, we have developed the J-OC-PSP ( = J-OC-OC-PSP: Decomposition of J into Orbital Contributions using Orbital Currents and Partial Spin Polarization) method and applied it to a variety of SSCC problems. J-OC-PSP is based on a decomposition of the SSCC into one-, two-, and n-orbital contributions. It can be applied to all four Ramsey terms of the coupling mechanism, namely the Fermi contact (FC), spin dipole (SD), paramagnetic spin-orbit (PSO), and the diamagnetic spin orbit (DSO) part where one can distinguish between one- and two-electron interactions. Results of the analysis are presented in terms of spin density, orbital current, and energy density distributions. This helps to understand, which orbitals are actively or just passively transferring spin information between the coupling nuclei. Using localized molecular orbitals (LMOs) as suitable descriptive tools, one can study the contribution of the bond LMOs in dependence of atom electronegativity and bond polarizability, the influence of lone pair LMOs on the coupling mechanism, the passive but nevertheless important role of p-orbitals for spin transport, the description of multiple bonding and p-delocalization by the non-contact terms, or rear lobe interactions of bond LMOs in saturated molecules. Also, general mechanistic features such as through-bond and through-space coupling, across-H-bond coupling, long-range coupling, and multi-path coupling can be efficiently analyzed in this way.
D. Cremer and J. Gräfenstein, Calculation and Analysis of NMR Spin-Spin Coupling Constants, Feature Article, Phys. Chem. Chem. Phys. 9 (2007) 1-26.
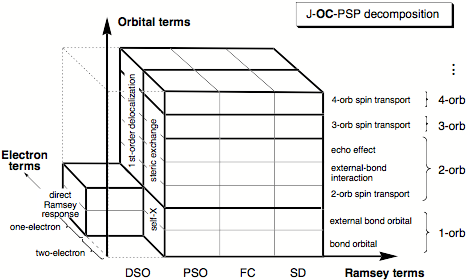
Figure 1. J-OC-PSP decomposition criteria I (Ramsey terms), II (orbital terms), and III (electron terms) of the SSCC shown in three-dimensional space. Abbreviation orb denotes the term orbital.
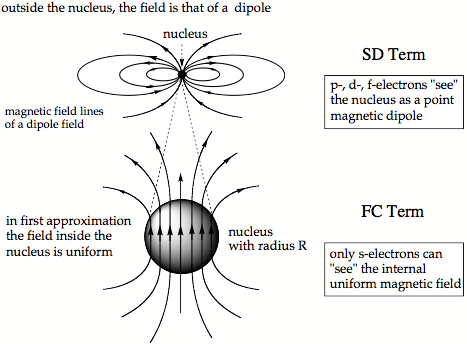
Figure 2. Magnetic field of a finite nucleus with radius R. In the lower part of the drawing, the nucleus with radius R is enlarged to see the internal uniform magnetic field.
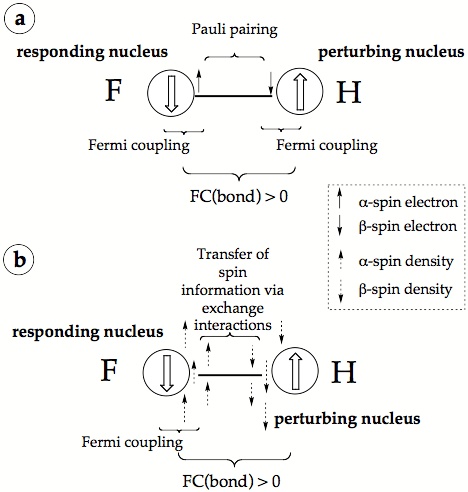
Figure 3. Dirac Vector Model of spin-spin coupling a) in the form normally presented in the literature, b) in a revised form, which explains the driving force of the FC coupling mechanism. The nuclear spin is indicated by large up (a) and down (ß) arrows surrounded by a circle symbolizing the finite size of the nucleus.
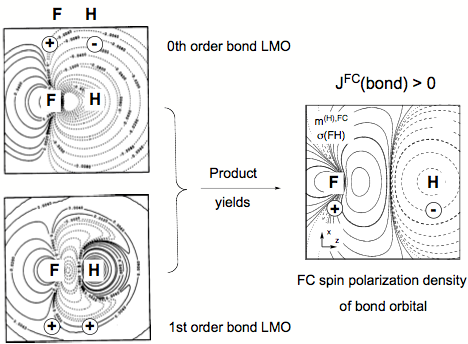
Figure 4. FC spin polarization density distribution of the FH bond orbital (right side) generated by multiplying the zeroth order bond orbital (upper left) with the corresponding first order orbital (lower left) all given in form of contour line diagrams. Solid contour lines of the FC spin polarization density distribution indicate a, dashed contour lines ß FC spin polarization density. For the LMOs, solid (dashed) contour lines denote positive (negative) amplitudes. The signature of LMOs and FC spin polarization density at the coupling nuclei is indicated.
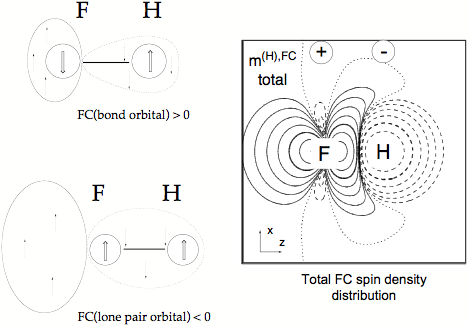
Figure 5. Total FC spin polarization density distribution of the FH coupling constant given in form of a contour line diagram. Solid contour lines of the FC spin polarization density distribution indicate a, dashed contour lines ß FC spin polarization density. The signature of the FC spin polarization density at the coupling nuclei is indicated. The major contributions to the total FC spin polarization density result from the bond orbital and the s lone pair orbital. The signs of these contributions are given by the extended Dirac Vector diagrams on the left side of the drawing.
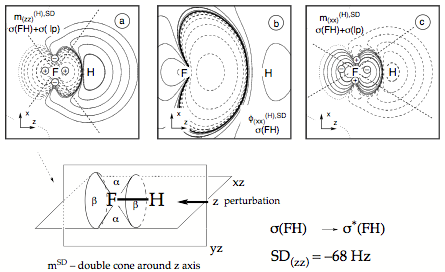
Figure 6. Analysis of the SD term of the SSCC1J(FH) calculated at the CP-DFT/BLYP(60:40) level of theory. (a) Contour line diagram of the SD spin polarization density distribution of the (zz) subcomponent for the contribution from the bond and σ lone-pair orbitals. (b) SD first-order bond orbital σ(FH) calculated for the (xx) subcomponent. (c) SD spin polarization density of the (xx) subcomponent for the contribution from the bond and σ lone-pair orbitals. Solid contour lines indicate positive, dashed contour lines negative values. The signature of the quadrupole potential at the responding nucleus F is indicated in Figures a) and c). - The drawing in the lower part gives schematically the double cone of the spin polarization density oriented along the bond axis (z-direction) as caused by the bond orbital.
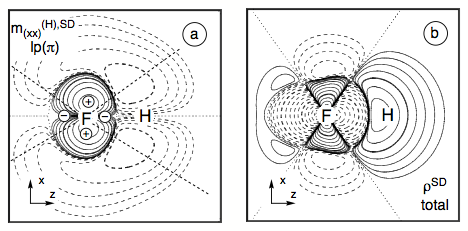
Figure 7. Analysis of the SD term of the SSCC1J(FH) calculated at the CP-DFT/BLYP(60:40) level of theory. (a) Contour line diagram of the SD spin polarization density distribution of the (xx) subcomponent for the contribution arising from the lone pair pπ(F) orbital. (b) Total isotropic SD energy density distribution of the FH coupling constant given in form of a contour line diagram. Solid contour lines indicate positive, dashed contour lines negative values. The signature of the quadrupole potential at the responding nucleus F is indicated in Figure a).
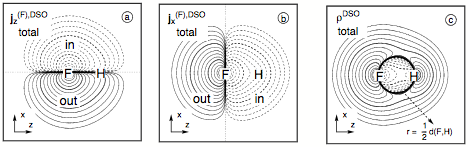
Figure 8. Analysis of the DSO term of the SSCC1J(FH) calculated at the CP-DFT/BLYP(60:40) level of theory. Contrary to the contour line diagrams shown for the spin polarization terms, the F nucleus is chosen as the perturbing nucleus. The position of F and H nucleus in the drawing plane are indicated by the element symbols. Contour levels chosen in geometric progression with a factor of 1001/5 between neighboring contour lines. Solid (dashed) lines refer to positive (negative) scalar densities or current densities out of (into) the drawing plane (indicated by "out" or "in"). Contour lines for 0.1 and 10 are printed in bold. All densities scaled by a factor of 10. (a) Total DSO current density distribution j(F),DSO for the perturbation in z direction. (b) Total DSO current density distribution j(F),DSO for the perturbation in direction. (c) The total isotropic DSO energy density distribution ρDSO.
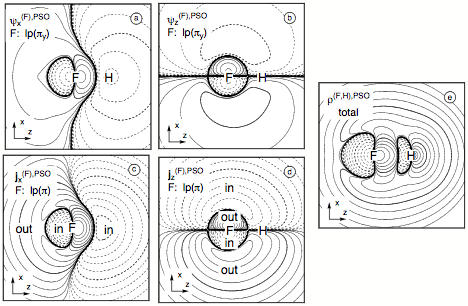
Figure 9. Analysis of the PSO term of the SSCC1J(FH) calculated at the CP-DFT/BLYP(60:40) level of theory. Contrary to the contour line diagrams shown for the spin polarization terms, the F nucleus is chosen as the perturbing nucleus. The position of F and H nucleus in the drawing plane are indicated by the element symbols. Contour levels chosen in geometric progression with a factor of 1001/5 between neighboring contour lines. Solid (dashed) lines refer to positive (negative) scalar densities or current densities out of (into) the drawing plane (indicated by "out" or "in"). Contour lines for 0.1 and 10 are printed in bold. All densities scaled by a factor of 10. (a) PSO first-order πy(F) lone pair LMO given for the perturbation in x direction. (b) PSO first-order πy lone pair LMO given for the perturbation in z direction. (c) PSO current density distribution from the two (π) lone pair LMOs in the xy plane for the perturbation in x direction, thus leading to a current in the yz plane. (d) PSO current density distribution from the two π(F) lone pair LMOs in the xy plane for the perturbation in z direction, thus leading to a current in the xy plane. (e) Total PSO energy density distribution for the responding nucleus H.
