II) Nanotechnology Related Research
II) Nanotechnology Related Researc
1. Development of Software for Calculating Nanostructures
1.1 Design of XC functionals for Use in Computational Nanotechnology
DFT with standard XC functionals is only partially satisfactory when calculating band structures of metals and, especially, semiconductors. Standard DFT fails even totally when describing van der Waals complexes (physisorption), which is well-known in the community of quantum chemists and solid state physicists, but for some reasons however not considered in the DFT investigations focusing on SWCNT complexes. [15]
a) Hybrid exchange functionals perform reasonably for band structure calculations in semiconductors but are too expensive numerically (because of the inclusion of some exact exchange) for large scale calculations as planned in this work. The mixing of exact and DFT exchange can be realized more economically by using a screened exchange functional [21] in which the two-electron operator is split into a short range part (SR, described by standard DFT exchange-functionals) and a long range part (LR, described by exact exchange) with the help of an error function. This splitting reduces the computational cost while keeping the advances of the hybrid approach so that band gap values can be calculated with convincing accuracy. We will program the HSE03 [21] functional and fine-tune it for the description of SWCNTs.
b) In the case of van der Waals complexes, our approach will be based on the consideration that for a correct description of van der Waals interactions (a) exchange repulsion (exaggerated by DFT) must be fine-tuned, (b) dispersion interactions (lacking in DFT) must be added, and (g) electrostatic interactions must be optimized via a suitable basis set. Problem a) will be solved with a long-range exact exchange (LR, see above) following Gill and others [22]. The correct description of the dispersion forces can be accomplished by adding a R–6 term as suggested by Andersson, Lundqvist, and Langreth (ALL) [23]. Finally we will use Hirao’s concept [24] of a one-parameter progressive (OP) correlation functional to describe equal and opposite spin correlation in a balanced way. The LR-BOP+ALL functionals are at the moment the functionals with the largest potential in terms of accuracy and general applicability and we will fine-tune them to the CNT problems of this proposal by optimizing the necessary empirical parameters and programming ALL for our COLOGNE program [25].
1.2 Development of a SCC-TB-DFT Program for Computational Nanotechnology
We will develop a tight-binding SCC-TB-DFT program [26] to calculate CNT geometries using moderate basis sets of split valence and augmented split-valence quality. The SCC-TB-DFT approach has the advantage of being rather economic (one fifth of the time of a DFT calculation) and also leading to reasonable geometries. For reference calculations at a higher level of DFT, we will use the packages PWSCF [27] and SIESTA [28].
Band structure calculations: Although this is a routine task in solid state physics predominantly carried out at the HF or DFT level, the accuracy, especially with regard to band gaps, obtained in these calculations is mostly not acceptable for a quantum chemist. In this project, we will invest into the fine-tuning of the exchange-correlation (XC) functional. Our starting point will be the HSE03 functional [21], which is a screened XC functional replacing the more costly hybrid functionals and leading to errors in 0.1-0.2 eV range (rather than 1-2 eV as observed with standard XC functionals). In all these calculations we will use periodic boundary conditions as realized in most solid state programs. These calculations will be done with the COLOGNE package [25]. Benchmark calculations with conventional hybrid functionals will be done with the CRYSTAL03 package. [29]
Conductivity calculations (determination of current/voltage characteristics): The I-V characteristics will be calculated with the help of non-equilibrium Green function theory merged into DFT as described by Brandbyge et al. [30] in their theory of non-equilibrium electron transport. This approach allows treating the transport of negative (positive) charge in molecular-electronic devices connected to two semi-infinite electrodes that may be at different Fermi levels. Both the electrodes and the device are described at the atomic level. Also, the potential distribution within the device and the transmission coefficient in dependence on the electron energy will be calculated. As appropriate software the TranSIESTA-C code will be used [31].
2. Investigation of Carbonnanotubes
If one considers which research areas in physics, chemistry, and engineering experienced the strongest growth in the last ten years, then molecular materials science and nanotechnology have to be mentioned first. Actually, material science was always an active research field and there was quite early science that worked with structures in the nano-scale range. However, previously, materials science was a research field dominated by physics and engineering, driven by the attempts in computer and information technologies to miniaturize transistors and electronic processors. It was essentially a top-down strategy: one starts with a macroscopic device and one tries to make it smaller and smaller. This approach has found its complement in the 90ies. There is now a molecular branch of materials science and nano-technology, which follows a bottom-up strategy. Atoms and molecules are manipulated in such a way that they form by self-assembly and self-organization nano structures with defined properties. The goals of molecular material science (MMS) and molecular nanotechnology (MNT) reach from nano-electronics to quantum computing, molecular motors, bioimaging, and biosensors. [1] The importance of the field is reflected by the amount of money invested by the leading science nations into MMS and MNT. For example, the US government allocated 2006 more than 1 billion dollars to nanotechnology [2] and similar high sums are invested in Europe and in Japan.
In this connection it has to be stressed that research in MMS and MNT is not just a matter of good will and sufficient funding. MMS and MNT are essentially interdisciplinary research fields combining research activities in physics, engineering, chemistry, biology, and medicine. Accordingly, research in these fields requires a broad scientific background and working practice in several disciplines of natural sciences. In addition, the nano-sciences offer a multitude of research avenues, many of which may turn out in the future as dead ends. Therefore, guidance of practical research by theoretical means is absolutely necessary. The nature of the objects that MMS and MNT are dealing with makes computational physics, quantum chemistry, and theoretical modeling extremely important.
Our research focuses on the design of new nano-electronic devices utilizing the extraordinary properties of single-wall carbon nanotubes (SWCNT). The design work will comprise the exploration of a systematic functionalization concept for SWCNTs, the description of possible junctions between semiconducting and metallic parts of a nanotube (NT), and the construction of nano-electronic devices with the help of computational physics and computational chemistry.
Avouris, IBM
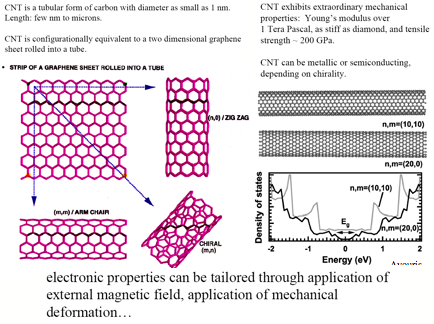
2.1 Systematic Generation of Junctions within a SWCNT
The basic design strategy of this proposal is to generate both metallic and semiconducting sections on a single SWCNT using different functionalization techniques.
Different functionalization strategies for SWCNT’s will be investigated in this work: (a) Intrinsic functionalization by varying the tube diameter – (b) Chemical bonding at the SWCNT surface either on the outside, at the inside, or both – (c) Van der Waals complexation of a SWCNT by aromatic compounds – (d) Intercalation by hydrogen, alkali metals, and transition metals, the latter in form of wires – (e) External adsorption of metal particles (nano-dots or nano-wires) – (f) Defect generation and doping of a SWCNT.
A large number of both theoretical [3] and experimental [see e.g. 3,4,5,6] investigations have shown that functionalization can change the band structure of a NT and thereby its metallic or semiconducting properties. So far there is no general rationale how different kinds of functionalization influence the electronic structure of a SWCNT. Theoretical work has been flawed by the fact that the electronic structure of SWCNT is poorly described by standard DFT methods. Even less is known about the properties of junctions between differently functionalized parts of a SWCNT. The major goal of this project is to gain an insight into the electronic properties of a differently functionalized SWCNT and to explore the electronic processes that can occur at one or more junction between different segments of a NT using refined DFT methods.
For the semiconducting sections, different band gaps can be realized, and the conduction type (p, n, or intrinsic) can be adjusted by using the various functionalization concepts. Experimental work gives some suggestions in this respect. A p-n-p junction, e.g., has been synthesized [5] by first coating a p-semiconducting SWCNT (due to contaminations) by polymethylmethacrylate and then using electron beam lithography to open a window that was then doped by K vapor. In this way, an n-type area was generated located between p-type areas so that a p-n-p junction on a SWCNT was realized that should possess the properties of a quantum dot. From a modeling point of view, this experiment is less suited for building up a new design concept than the following one.
Kim et al. [4] described a particularly attractive way of segmented functionalization by burying one half of a SWCNT in SiO2 and hydrogenating the other half (using hydrogen gas at elevated temperatures). In this way, these authors could generate a semiconducting (hydrogenated) and a metallic part (non-hydrogenated) on one SWCNT. It is obvious that this recipe can be generalized by using different burying materials and different gases that react with the CNT, however, not with the burying material (e.g., F2 cannot be used because it reacts also with SiO2). We use the experiment by Kim et al. as a suitable starting point for our design concept. Accordingly, we will investigate SWCNTs with one or more junctions between functionalized (hydrogenated, halogenated, etc.) and non-functionalized segments.
For the purpose of obtaining p-type and n-type semiconductors of different quality, we will use selective intercalation by alkali and halogen atoms (one segment contains a string of alkali atoms and becomes an n-conductor, another a string of (non-reacting) halogen atoms and becomes a p-conductor. In this way the experiment of Ref. [4] will be modeled in a different way.

2.2 Design of Nano-Devices
Using the functionalization strategies of 1) and 2), we will design typical nano-electronic devices that parallel conventional electronic devices. Bearing the small device size in mind, we will have to explore the consequences of quantum effects: For instance, a narrow semiconducting segment between two metallic ones allows for tunneling and thus the generation of negative dynamic resistance. We will try to realize a number of devices, classified in the following according to the sequence of semiconductor (S) and metallic (M) parts along the tube.
SM: The simplest possible device consists of an interface between a S and a M segment. For a properly chosen S segment, this junction is rectifying, i.e. a counterpart to a conventional Schottky diode. We will try various combinations (see above) and calculate the current-voltage (I-V) characteristics.
MSM: Typically, electronic devices will have the structure MSM, i.e. the semiconducting part sandwiched between two metallic parts. Depending on the structure of the S part, the following devices will arise. Intrinsic S: The device can provide tunneling between the M electrodes. The I-V characteristic will depend largely on the tails of the orbitals from the metallic into the semiconducting region. A simple tunneling device with negative dynamic resistance can be realized in this way, which is e.g. interesting for high-frequency oscillators. - p- or n-S: If the semiconducting channel is p- or n-conducting, the device can serve as the basis for a FET (field effect transistor). The device has then to be completed by an external isolated gate electrode. Both p- and n-FETs should be studied to lay the basis for a nanoscale realization of CMOS circuits (the backbone of current microelectronics). - Sequence pn: This will provide the counterpart to a conventional pn diode. - Sequence p+p or n+n: (Comment: p+ means strongly p-conducting) For proper doting of the semiconductor, one contact becomes Ohmic, the other rectifying. This is a Schottky diode with two metallic contacts. - Sequence pnpn: This provides a device with a dynatron I-V characteristic, i.e. a characteristic with negative hysteresis. A pnpn diode can be used as a simple one-component memory element.
SMS: If a metallic segment is enclosed within two semiconducting ones, one gets a quantum dot. Alternatively, a narrow-gap semiconducting part can be enclosed between two wide-gap ones. Among others, quantum dots may be interesting as building blocks for memory devices or as realizations of qubits for quantum computing.
2.3 Determination the Magnetic Properties of CNT
There have been NMR investigations on CNT in both the solid and the solution state. In general, NMR signal measurement is hampered by chemical shift dispersion reflecting a distribution of diameter and helicity, chemical shift anisotropy, bulk magnetic susceptibility, dipole-dipole interactions between 13C nuclei (also 13C and 1H spins at defects or edges), Knight shift interactions from metallic contaminations or interactions with conducting electrons. By MAS NMR spectroscopy some of these problems can be eliminated, however sample purity as the major problem remains. So the importance of CNT NMR spectroscopy is still behind that of fullerene NMR spectroscopy, but will rapidly increase in the way functionalization of CNT progresses and pure samples in solution are available. Nevertheless it has been already shown the 13C chemical shifts reflect the metallic or semiconducting nature of SWCNT. [20]
We will calculate NMR chemical shifts and spin-spin coupling constants and analyze them to obtain electronic structure descriptors. In this way we will continue recent work on (n,n) SWCNTs, for which we have shown that NMR spin-spin coupling constants indicate are a sensitive probe for local (diamagnetic) currents and a direct measure for the band gap.
For this purpose the program COLOGNE [25] will be used, which can determine chemical shifts and NMR spin-spin coupling constants for large molecules using coupled perturbed DFT with specially designed XC functionals. Especially the program J-OC-PSP
References for 1 and 2
- [1]See e.g. R. H. Boughman et al., Science 297, 787 (2002); K.L. Wang, J. Nanosc. Nanotechn. 2, 235 (2002); V. Balzani et al., ChemPhysChem 4, 49 (2003); Gooding et al., Electroanalysis 15, 81 (2003); N. C. Seeman, Rep. Progr. Phys. 68, 237 (2005).
- [2]National Science Foundation Report, USA, 2004.
- [3]See e.g. J. Zhao et al., J. Phys. Chem. B 108, 4227 (2004); H. Pan, Phys. Rev. B 70, 245425 (2004); O. Gülseren et al., Phys. Rev. B 66, 121401 (2002).
- [4]K. S. Kim, Curr. Appl. Phys. 4, 559 (2004).
- [5]J. Kong et al., Appl. Phys. Lett. 80, 73 (2002).
- [6]E.T. Mickelson, Chem. Phys. Lett. 296, 188 (1998).
- [7]C. Bauschlicher, Nano Lett. 1, 223 (2001).
- [8]K. Kudin et al., Phys. Rev. B 63e, 045413 (2001).
- [9]H. Bettinger, ChemPhysChem 4, 1283 (2003).
- [10]E. Zurek et al., J. Am. Chem. Soc. 126, 13079 (2004).
- [11]Y. Zhang et al., Chem. Phys. Lett. 331, 35 (2000).
- [12]C.K. Yang et al. Phys. Rev. B 66, 041403 (2002).
- [13]Y. Yagi et al., Phys. Rev. B 69, 075414 (2004).
- [14]Y.J. Kang et al., Phys. Rev. B 71, 115441 (2005).
- [15](a) J. J. Zhao et al., Appl. Phys. Lett. 82, 3746 (2003). (b) P. Giannozzi, Appl. Phys. Lett. 84, 3936 (2004).
- [16]I. Willner et al., ChemPhysChem 5, 1084 (2004).
- [17]M. Hirscher et al., J. Nanosci. Nanotechn. 3, 3 (2003); S. S. Han et al., Carbon 42, 2169 (2004).
- [18]J. Li et al., J. Chem. Phys. 119, 2376 (2003); H. Cheng et al., J. Chem. Phys. 120, 9427 (2004) (comment); J. Li et al., ibid. p. 9430 (reply).
- [19]E. Yoo et al., J. Phys. Chem. B 108, 18903 (2004).
- [20]S. Latil et al., Phys. Rev. Lett. 86, 3160 (2001).
- [21]J. Heyd et al., J. Chem. Phys. 118, 8207 (2003).
- [22]R.D. Adamson et al., Chem. Phys. Lett. 254, 329 (1996).
- [23]Y. Andersson et al., Phys. Rev. Lett. 76, 102 (1996).
- [24]T. Tsuneda et al., J. Chem. Phys. 110, 10664 (1999).
- [25]E. Kraka et al., COLOGNE05, Göteborg University, Sweden, 2005.
- [26]M. Elstner et al., Phys. Rev. B 58, 7260 (1998).
- [27]S. Baroni et al., PWSCF Version 2.1.2, DEMOCRITOS, Trieste, Italy, 2005.
- [28]J.M. Soler et al., J. Phys.: Cond. Matt. 14, 2745 (2002).
- [29]V. Saunders et al., CRYSTAL03, University of Torino, Italy, 2003.
- [30]M. Brandbyge et al., Phys. Rev. B 65, 165401 (2002).
- [31]TranSIESTA-C, Version 1.3, Atomistix A/S, Copenhagen Denmark, 2005.
