II) Nanotechnology Related Research
II) Nanotechnology Related Research
- Determination of the NMR parameters of Spherical Fullerenes
- Investigation of the Formation and Structure of Colloidal Quantum Dots
3. Determination of the NMR parameters of Spherical Fullerenes
The discovery of a new form of elementary carbon in the 80ies has initiated a new field in chemistry and is one of the reasons for the current large interest into nanotechnologies. Intense efforts have been made to unravel the electronic structure and the properties of fullerenes. In this connection, NMR spectroscopy has and is still playing a key role because by the number of NMR signals one can get information on the symmetry of the fullerene under investigation, by the chemical shifts on the degree of electron delocalization, and by the NMR spin-spin coupling constants on the topology and the nature of bonding. For example, the NMR spectrum of C60 fullerene consists of a single line at 143 ppm demonstrating the equivalence of all C atoms and the aromatic character of bonding.
There is a large potential of NMR spectroscopy in this field, which however is hampered by the fact that the large multitude of signals for less symmetric fullerenes combined with the fact that all lines appear in a small region typically of aromatic C atoms. This is a situation, in which our CP/DFT approach for calculating NMR spin-spin coupling constants (SSCCs) is of large value because it can complement the information gained from NMR measurements to a complete picture with all SSCCs and chemical shifts. Agreement between the available measured and the corresponding calculated SSCCs suggests that all additional SSCCs are reliable and that the complete set of NMR parameters provides a detailed description of the electronic structure, bonding, p-delocalization and other properties of the fullerene investigated. Our work will concentrate on medium-size fullerenes such as C76, C78, C82, and C84, (considering the various isomers), which are found as extracts of the soot obtained by resistive heating, contact-arc vaporization, in benzene-oxygen flames or as products of plasma vaporization of graphite. For testing the reliability of the SSCCs calculated, we will use C70, for which an experimental NMR spectrum is available, as reference. Calculations will be carried out with our CP-DFT/SSCC method at the CP-DFT/B3LYP and BPW91 levels of theory using VDZ basis sets augmented in the core region by extra functions.
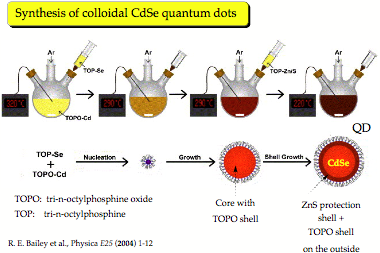
4. Investigation of the Formation and Structure of Colloidal Quantum Dots
(Michael Filatov, Dieter Cremer)
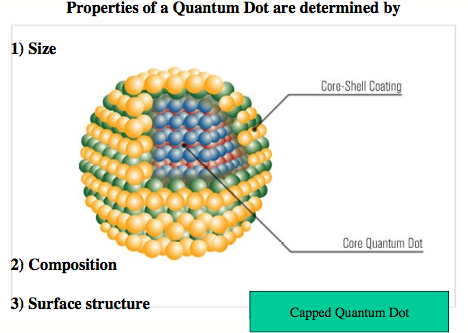
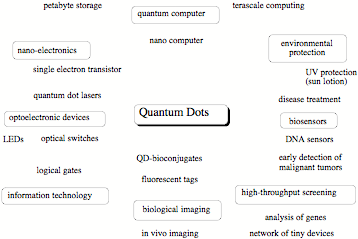
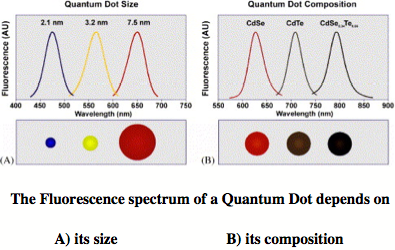
A colloidal quantum dot is a fluorescent nanostructure containing from a few tens to several thousands atoms and a certain number of free electrons. [1] Because of the size limitation of a quantum dot, the free electrons occupy discrete energy levels rather than energy bands as is typical of bulk matter (although with increasing number of energy levels the band structure becomes again obvious for large quantum dots). Colloidal quantum dots change their color and other properties in dependence of their size, composition, and surface characteristics. Quantum dots are major research objects in molecular nanotechnology because of their wide applicability, from nano-electronics to optical devices, information technology, and quantum computing. Most exciting is the use of quantum dots as biosensors and for biological imaging, which is of utmost importance in connection with the monitoring of environmental pollution or national security (direct detection of toxic gases). High-throughput screening, gene analysis, disease diagnosis, or medication control all advance rapidly with the help of quantum dots. [1]
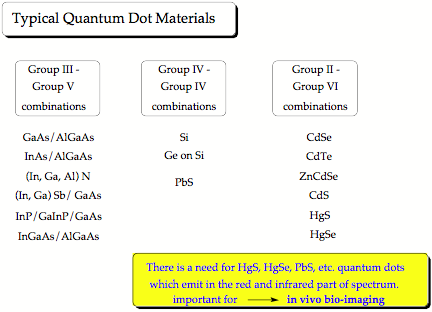
The first colloidal quantum dots were CdSe nano-crystals, which belong to the type IIb/VI quantum dots (Zn, Cd or Hg chalcogenides). [1] Today, we are especially interested in quantum dots made from PbS, HgS or HgSe. These emit light in the red and infrared spectrum, [2] which can penetrate several layers of tissue, so that biological processes or the action of a drug can be followed in vivo. We are investigating clusters of IIb-chalcogenides, especially HgS, HgSe, and HgTe to determine the properties of the corresponding colloidal quantum dots. Our previous work on mercury oxide and sulfide revealed that some of their fundamental chemical properties considered to be understood for decades are actually based on erroneous data and that the chemistry of these compounds still needs to be explored. [3,4]
Our research program comprises the following steps: 1) Quantitative determination of binding energy, geometry, vibrational frequencies, charge distribution, multipole moments, ionization potential, electron affinity, EPR hyperfine coupling constant for cation and radical, vertical and adiabatic excitation energies of IIb/VI monomers, dimers, trimers, etc. up to clusters of 100 and more atoms composed of Zn, Cd, Hg and O, S, Se, Te (IIb chalcogenides) using quantum chemical methods; 2) For the smaller clusters we will employ Coupled Cluster theory and search for the most stable isomeric forms, whereas for the larger clusters we will use MP Perturbation Theory and Density Functional Theory and use forms that resemble the crystal structure of the compounds in question (Wurtzite or Zincblende lattice). We will, where possible, compare coupled cluster with DFT results to find the best exchange-correlation functional for describing larger clusters; 3) Analysis of the cluster properties in dependence of composition, structure, and size with the goal to extrapolate them to clusters of large size that resemble quantum dots; 4) Investigation of the surface properties and the binding possibilities of quantum dots using cluster models developed in steps 1) to 3); 5) Discussion of the use of IIB/VI quantum dots for bioimaging and biosensing purposes; 6) Extension of this work to PbS and PbSe.
The investigation of the IIb and Pb-chalcogenides requires relativistically corrected ab initio calculations based on Many Body Perturbation or Coupled Cluster theory. In general, this implies difficult and costly calculations, which we will circumvent by using our methods –based on the regular approximation (RA) [5] to the exact relativistic Hamiltonian and the Normalized Elimination of the Small Component (NESC) approach. [6-12] Originally, the RA [5] suffered from a) a gauge dependence problem, b) the fact that it could only be applied in a numerical fashion at the DFT level of theory, and c) that its extension to the exact Dirac description was unclear. We were able to improve the RA in an elementary way by a) solving the gauge dependence problem, [12] b1) deriving for the first time a compact analytical representation of the RA that makes its applicable to all wave function (Hartree Fock, Configuration interaction, Many Body Perturbation theory, Complete Active Space SCF, Coupled Cluster with single, double, and triple excitations, etc.) and density functional methods (LDA, GGA, hybrid XC, CASDFT), [8] b2) deriving analytical energy derivatives within these methods for property calculations, [8] and c) demonstrating that the RA leads in higher order directly to the NESC method [10,11] and thereby to the exact Dirac result for a given level of correlation corrections. We programmed the following new methods (from less to more accurate): matrix-ZORA (zeroth order RA), ZORA-GI (gauge independent ZORA), matrix-IORA (infinite order RA), IORA-GI, IORAmm (IORA with metric matrix), scaled IORA, and NESC-SORA (NESC with the second order regular approximation). [6-12] NESC-SORA leads to results close to the exact Dirac values and is more accurate than fifth order DKH (Douglas-Kroll-Hess) theory where we obtain this accuracy at less than 50% of the cost of fifth order DKH. [11].