RING is a coordinate transformation program written to provide the quantitative data that aids the interpretation of ring conformations and planar ring forms. Starting from the normal mode analysis of an N-membered ring (N-ring), one can show that always N-3 vibrations describe the out-of-plane puckering of the N-ring and 2N-3 vibrations in-plane deformations. Based on this analysis RING provides the following information once the Cartesian coordinates of the ring molecule have been read in:
- Ring puckering coordinates
- Ring deformation coordinates
- Ring substituent orientations (axial, equatorial, etc.)
- Orientation of mean plane and least-squares plane
This information is needed for conformational and electronic structure analysis of ring molecules:
- Description of non-planar ring conformations of specific pucker
- Expressing a given ring conformation in terms of basis conformations
- Description of conformational processes such as ring pseudorotation, ring inversion, etc.
- Description of the conformational energy hyper-surface and the associated potential
- Determining the position of substituents in a quantitative rather than qualitative way
- Quantitative description of the deformation of the planar ring relative to the reference polygon
- Description of bond-pseudorotation and other dynamic processes of planar ring molecules such as bond shifting
- Quantitative description of ring substituent effects
- Quantitative description of ring opening processes in molecules
Relevant literature (see list of publications): A) Theory
- A1)A General Definition of Ring Puckering Coordinates, D. Cremer and J.A. Pople, J. Am. Chem. Soc. 97, 1354-1358 (1975).
- A2)RING - A Coordinate Transformation Program for Evaluating the Degree and Type of Puckering of a Ring Compound, D. Cremer, Quantum Chemical Program Exchange, No. 288, 1-8 (1975).
- A3)A General Definition of Ring Substituent Positions, D. Cremer, in "Stereochemistry and Conformational Analysis", Israel J. Chem. 20, 12-19 (1980).
- A4)On the Relationship between the Mean Plane and the Least-Squares Plane of an N-membered Puckered Ring, H. Essen and D. Cremer, Acta Cryst. B40, 418-420 (1984).
- A5)On the Correct Usage of the Cremer-Pople Puckering Parameters as Quantitative Descriptors of Ring Shapes - A Reply to Recent Criticism by Petit, Dillen, and Geise, D. Cremer, Acta Cryst. B40, 498-500 (1984).
- A6)Calculation of Puckered Rings with Analytical Gradients, D. Cremer, J. Phys. Chem. 94, 5502 (1990).
Relevant literature (see list of publications): B) Applications
- B1)Molecular Orbital Theory of the Electronic Structure of Organic Compounds. 23. Pseudorotation in Saturated Five-Membered Ring Compounds, D. Cremer and J.A. Pople, J. Am. Chem. Soc. 97, 1358-1367 (1975).
- B2)Theoretical Determination of Molecular Structure and Conformation. 3. The Pseudorotation Surface of 1,2,3-Trioxolane and 1,2,4-Trioxolane, D. Cremer, J. Chem. Phys. 70, 1898-1910 (1979).
- B3)Theoretical Determination of Molecular Structure and Conformation. 4. Electronic Effects Influencing the Stability of Methyl Substituted Primary Ozonides, D. Cremer, J. Chem. Phys. 70, 1911-1927 (1979).
- B4)Theoretical Determination of Molecular Structure and Conformation. 5. Electronic Effects Influencing the Stability of Methyl Substituted Final Ozonides D. Cremer, J. Chem. Phys. 70, 1928-1936 (1979).
- B5)Theoretical Determination of Molecular Structure and Conformation. 11. The Puckering of Oxolanes, D. Cremer, in "Application of Theory to Organic and Organo-metallic Molecules", Israel J. Chem. 23, 72-84 (1983).
- B6)Theoretical Determination of Molecular Structure and Conformation. 12. Puckering of 1,3,5-Cycloheptatriene, 1H-Azepine, Oxepine, and their Norcaradienic Valence Tautomers, D. Cremer, B. Dick, and D. Christen J. Mol. Struct. 110, 227-291 (1984).
Relevant literature (see list of publications): C) Reviews
- C1)Ab initio Studies of Six-Membered Rings, Present Status and Future Developments, D. Cremer and K.J. Szabó, Methods in Stereochemical Analysis, Conformational Behavior of Six-Membered Rings, Analysis, Dynamics, and Stereoelectronic Effects, E. Juaristi, Editor, VCH Publishers, 1995, p. 59.
A) Ring puckering: Description of the non-planar conformations of the N-ring
For a set of N-3 out-of-plane vibrations with finite vibrational amplitude a puckered ring is exactly specified. The vibrational amplitudes correspond to the N out-of-plane coordinates zj, which in turn can be exactly specified by the puckering equations (1) and (2): [A1,A6,C1]
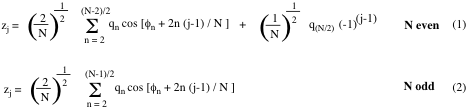
In these equations, the parameters qn correspond to puckering amplitudes and the angles φn to pseudorotation phase angles. The index n denotes the pseudorotation modes of the N-ring. In the derivation of the puckering coordinates, n = 0 and n = 1 correspond to translation and overall rotation of the planar reference ring in the mean plane. [C1] The 3-membered ring is always planar and does not possess any put-of-plane vibrations. Hence, it has only index n = 0 and n = 1, defining parameter q1 and rotational angle φ1 for translation and rotation. Puckering starts with the 4-membered ring (N-3 = 1: puckering amplitude q2, one out-of-plane vibration leading to “crown puckering”) and pseudorotation with the 5-membered ring (N-3 = 2: puckering amplitude q2 and pseudorotation phase angle φ2). For a complete pseudorotation cycle, the phase angle φ2 increases from 0 to 180 and 360°, which is identical to the 0° situation. Such a pseudorotation cycle is schematically shown in Figure 1 for the 5-ring [A1,A3,B2,B3]
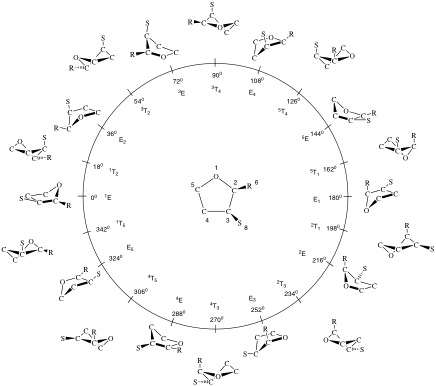
Figure 1. Pseudorotational cycle of tetrahydrofurane (O is atom #1; clockwise numbering around the ring). According to the rules for ring conformations (see below) the Cs-symmetrical envelope form with the O atom at the apex of the ring is located at φ2 = 0°. The C2-symmetrical twist form of tetrahydrofurane is located at φ2 = 90°. 10 envelope (E) and 10 twist (T) conformations are shown along a pseudorotation cycle (0° ≤ φ2 ≤ 360°) with fixed puckering amplitude q2. At the center of the pseudorotation cycle the planar form with q2 = 0 Å is located. Along the pseudorotation cycle an infinite number of forms are positioned where only the 20 E and T forms with the O atom at different ring positions are shown. A superscript before the symbol denotes for an E form that the apex atom is above the mean plane, a subscript behind E that the apex atom is below the mean plane. For the T forms, there is always a superscript before and a subscript behind T indicating the atoms of the bond with the largest dihedral angle where the first atom is above, the second atom below the mean plane. Note that φ2 values differing by 180° correspond to original and inverted form. The conformational space is N-3 = 2-dimensional. Substituents R and S are shown to indicate the different substituent orientations during pseudorotation.
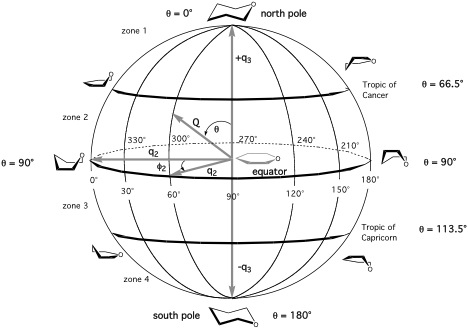
Figure 2. Conformational globe of a puckered six-membered pyran ring. Puckering coordinates {q2, φ2, q3} that span the globe as well as some distinct longitudes and latitudes are shown. The positions of distinct ring forms are shown in steps of 30° along the equator, the tropic of Cancer, and the tropic of Capricorn (compare with Figure 3). For reasons of clarity only the front side of the globe is shown. Conformations on the backside are shown in Figure 3. Atom O1 is always indicated.
A six-membered ring such as cyclohexane has 6-3 = 3 puckering coordinates, which split up into the pseudorotational coordinate pair {q2, φ2} describing the pseudorotation of boat and twistboat forms and a single “crown” puckering amplitude q3, which describes the chair form (positive q3) and the inverted chair form (negative q3). For pseudorotational cycles, the puckering amplitude is always positive.
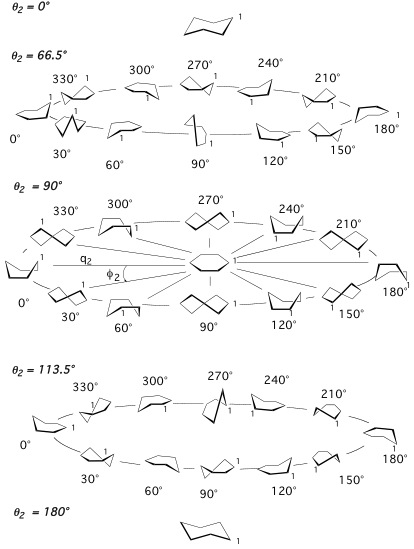
Figure 3. Conformations of puckered cyclohexane. Three pseudorotational cycles at the hyperspherical angles Θ2 = 66.5, 90, and 113.5° (compare with Figure 2) are shown. Distinct ring forms are shown in steps of 30° along the equator, the tropic of Cancer, and the tropic of Capricorn (compare with Figure 2).
A non-planar seven-membered ring has 7-3 = 4 puckering parameters spanning two different pseudorotational subspaces: {q2, φ2} and {q3, φ3}. The conformational energy space is 4-dimensional and its unit vectors, giving the location of the 7-ring boat, twistboat, chair and twistchair forms are orthogonal to each other. The conformational space can be symbolized by a torus as done in Figure 4.
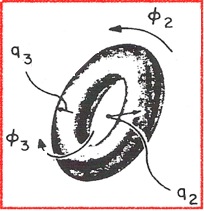
Figure 4. The pseudorotational cycles of a 7-membered ring symbolized by a torus.
In the 8-membered ring, there are these two pseudorotational spaces and an additional crown puckering space spanned by puckering amplitude q4.
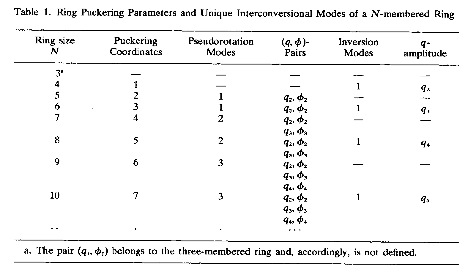
For even-membered rings, there are in general (N-4)/2 pseudorotational modes each described by a puckering angle – phase angle pair { qn,φn} where n = 2, 3, ... (N-2)/2. In addition, there is for even-membered rings an additional puckering amplitude qN/2, which describes crown puckering (N = 4: folding of the ring; N = 6: chair puckering, N = 8, 10, etc.: crown puckering).
For odd-membered rings, there are in general (N-3)/2 pseudorotational modes, again each described by a puckering amplitude – phase angle pair {qn,φn} where n = 2, 3, ... (N-1)/2. All ring conformations correspond to points in the (N-3)-dimensional conformational energy space.
Because of reasons of analysis, it is useful to use spherical (N = 6) or hyperspherical (N > 6) ring puckering coordinates {Q, Θn, φn} rather than the hypercylindrical coordinates {qn, φn} described above. For this purpose a total puckering amplitude Q is defined and a polar angle Θn (see Figures 2 and 3 for the six-membered ring). [A1,A3] These are also calculated by the program RING.
In Table 1 (taken from [A3]) the puckering coordinates are listed according to ring size.
The planar ring is the appropriate reference for the puckered ring. It is positioned in a plane, which is called the mean plane (zj = 0). There is a unique mathematical algorithm to determine the mean plane, which has been described elsewhere. [A1, A6] Each puckered ring is associated with a planar ring, which is obtained by projecting the puckered ring into the mean plane. The projected planar ring is described with a set of 2N-3 deformation parameters, which quantify the deviation of the planar ring from a regular N-membered polygon of unit length edges (see below).
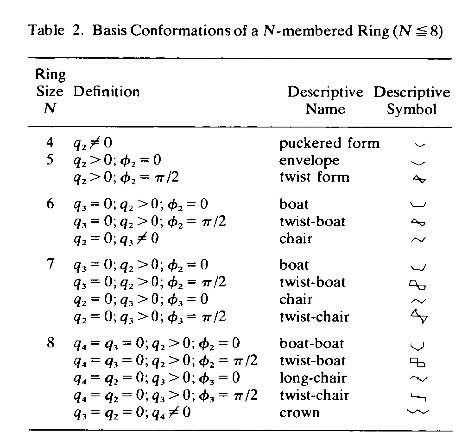
Definition of Basis Conformation: In the way the puckering coordinates span the conformational space of an N-membered ring they define basis conformations, which can be considered as the basis vectors of the conformational space. For this purpose, the puckering amplitudes are frozen at a constant value (larger zero) and the phase angles get values as defined in Table 2. In conformational analysis, one has given certain puckered ring forms with high symmetry common names reflecting the form of the puckered ring. Some of these forms turn out to be basis conformations (Table 2) whereas others are found on seminversion paths between pseudorotational cycles and inversion paths. In this way, conformational analysis is simplified because puckered ring forms can be related to each other via connecting paths through conformational space.
B) Ring deformation: Description of the deformation of the planar N-ring
(to be filled in after publication)
C) Ring Substituents: Description of the ring substituent orientations
Once the mean plane of a puckered ring has been determined, the orientations of the substituent bonds with regard to this plane can be determined. Those bonds, which are close to being perpendicular to the mean plane are called “g-axial” (g for geometrical) and those which are almost parallel to the mean plane “g-equatorial.”[A3] Substituent Bonds with an orientation being neither g-axial or g-equatorial but intermediate are termed “g-inclinal” (inclined with regard to the direction of the mean plane). These definitions generalize the Barton-Hassel-Pitzer-Prelog rules for the C-H bonds in cyclohexane [3] to all rings in a well-defined manner.
Program RING calculates the parameters α and ß that give the orientation of a substituent bond as illustrated in Figure 1. Of course the same description can be used for the ring bonds.
It is useful to distinguish between a top (t) and a bottom (b) side of the ring. Applying the rules for ring numbering, each atom gets a number. If looking at the ring and the atom numbers increase clockwise (counter-clockwise), the top side (bottom side) is seen.
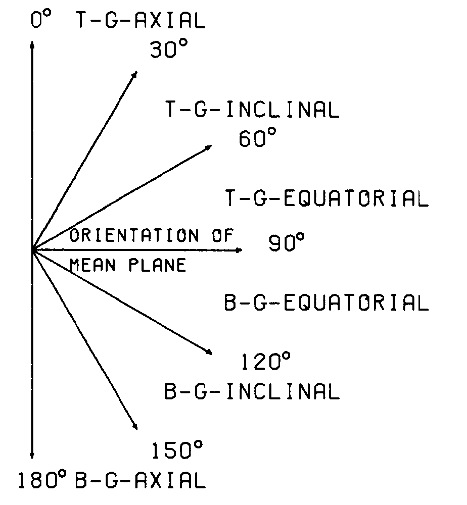
Figure 5. Definition of substituent orientations relative to the mean plane of the ring.
